Принято считать, что российский математик XIX века в своей теории заставил пересекаться параллельные прямые вопреки классической, евклидовой геометрии. Мы проверили, насколько справедливо это утверждение.
В известном романе Бориса Акунина «Турецкий гамбит» один из героев говорит другому: «Да кто вы такой, чтобы судить, кто несёт цивилизации благо, а кто гибель!? Государственный механизм он изучал, с вождями знакомился! А с графом Толстым, с Фёдором Михайловичем Достоевским вы познакомились? А русскую литературу вы читали? Что, времени не хватило? Дважды два это всегда четыре, а трижды три девять, да? Две параллельные прямые никогда не пересекаются? Это у вашего Эвклида они не пересекаются, а у нашего Лобачевского пересеклись!»
Аналогичное мнение в своё время высказывали такие известные люди, как писатели Александр Проханов, Евгений Водолазкин, Макс Фрай, журналисты Алексей Венедиктов и Юлия Латынина, политолог Леонид Радзиховский (хотя тот же Венедиктов позднее назовёт это конкретное высказывание глупостью), руководитель департамента здравоохранения Москвы Леонид Печатников, а также менее знаменитые деятели на страницах ТАСС, «Известий», на «Радио Свобода» и во многих других СМИ.
Для начала хотелось бы прояснить, в чём состоит утверждение о параллельных прямых из «Начал» Евклида — то самое, с которым поспорил Лобачевский в своей теории. Как пишет доктор физико-математических наук Владимир Успенский в своей книге «Апология математики», «практически все слышали про аксиому о параллельных прямых, ведь её проходят в школе». И абсолютное большинство опрошенных им на предмет её содержания случайных людей дали один и тот же чёткий ответ: аксиома состоит в том, что параллельные прямые не пересекаются.
Однако давайте заглянем в первоисточник. Первое систематическое изложение планиметрии (раздела геометрии, изучающего фигуры на плоскости) дал древнегреческий математик Евклид в его труде «Начала». В основу своей теории Евклид положил пять аксиом (или постулатов) — утверждений, не требующих доказательств.
1. От всякой точки до всякой точки можно провести прямую.
2. Ограниченную прямую можно непрерывно продолжать по прямой.
3. Из всякого центра всяким радиусом может быть описан круг.
4. Все прямые углы равны между собой.
5. Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых.
Ничего похожего на популярную формулировку, не так ли? Наше внимание мы обратим на пятый постулат, который в современных источниках часто формулируется так (подобную подачу приписывают Проклу, а также иногда называют аксиомой Плейфера): «В плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной».
А что такое параллельные прямые? По определению (а вовсе не по какой-либо аксиоме) это прямые, которые лежат в одной плоскости и не пересекаются. Таким образом, то, что огромное количество людей принимает за аксиому о параллельных прямых, является всего лишь их определением. А пресловутый пятый постулат Евклида выглядит совсем иначе.
Так что же сделал Николай Лобачевский? Многие его предшественники веками пытались доказать или опровергнуть пятый постулат Евклида, однако им для этого нужна была точка опоры, база, в качестве которой мог выступить только сам этот постулат. При этом на первый взгляд кажется, что его истинность очевидна. Однако 28-летний математик из Казанского университета не был в этом так уверен. Лобачевский попробовал заменить пятый постулат на его противоположность: «Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её».
Остальные четыре аксиомы Лобачевский не тронул. Математика интересовало, что будет после этого со всей системой геометрических теорем и иных утверждений, не вылезут ли противоречия, которые косвенно докажут, что предположение Евклида, пусть и недоказанное, было единственно и неизбежно верным. Но оказалось, что мир не рухнул. Все базовые утверждения классической геометрии прекрасно выстояли и на этом фундаменте.
Вот только зрительно представить подобную ситуацию достаточно сложно. Кто-то спросит: «А зачем её представлять? Важно, что в теории всё корректно» — и формально будет прав. Однако, по-видимому, иначе рассуждали члены учёной комиссии Казанского университета, прослушавшие доклад молодого математика 7 февраля 1826 года. Презентация работы под названием «Сжатое изложение начал геометрии со строгим доказательством теоремы о параллельных» провалилась, и рукопись даже не попала в печать.
Пройдёт три года, и Николай Лобачевский, теперь уже ректор университета, найдёт возможность опубликовать свой труд «О началах геометрии» в журнале «Казанский вестник». К сожалению, наука того времени ещё не была готова принять такой подход — в частности, работа удостоилась отрицательной рецензии Михаила Остроградского, одного из крупнейших русских математиков. И только несколько лет спустя на Лобачевского обратят внимание в Европе — в частности, «король математиков» Карл Фридрих Гаусс выдвинет его в члены-корреспонденты Гёттингенского королевского научного общества, а параллельно будет изучать идеи коллеги в оригинале, на русском языке. Сам Гаусс придерживался подобных идей, по его словам, уже много лет.
И только полтора десятилетия спустя появятся математические модели, в которых теория Лобачевского будет работать, не вызывая бесконечных споров. В частности, проективная модель, где за плоскость принимается внутренность круга, а за прямую — его хорда. В результате тот очевидный факт, что через одну точку, лежащую внутри круга, можно провести сколько угодно хорд, не пересекающихся с одной фиксированной хордой, в таких правилах игры становится иллюстрацией пятого начала геометрии Лобачевского. Другой пример реализации теории Лобачевского — псевдосфера, поверхность вращения кривой:
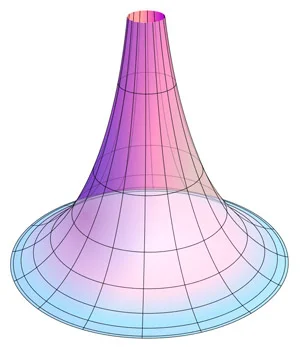
А в 1868 году выйдет доклад Бернхарда Римана, человека, который предложит свой подход в неевклидовой геометрии — несколько иной, нежели у Лобачевского. Однако успех его теории станет лишним подтверждением величия казанца, поскольку два математика сделали схожие шаги, только в разных пространствах. Если говорить математическими терминами, то у Евклида гауссова кривизна нулевая (1), у Лобачевского — отрицательная (2), у Римана — положительная (3):
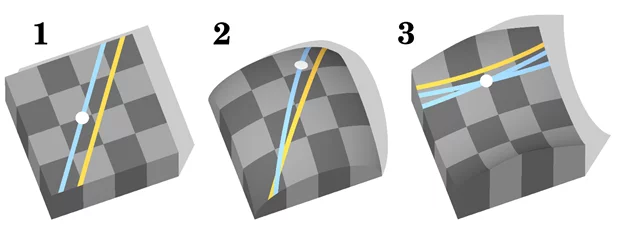
Но это совсем другая история, а здесь необходимо заключить, что в геометрии Лобачевского параллельные прямые тоже не пересекаются — ничего похожего русский математик не утверждал. В геометрии же Римана, вопреки утверждениям некоторых СМИ, просто нет параллельных прямых.
Неправда
Почитать по теме:
1. Всё параллельно. Как Лобачевский открывал свою геометрию
2. Параллельные прямые в мифологии, реальности и математике
Если вы обнаружили орфографическую или грамматическую ошибку, пожалуйста, сообщите нам об этом, выделив текст с ошибкой и нажав Ctrl+Enter.







