В сборниках занимательных фактов и прочей литературе нередко можно встретить утверждение о том, что в штате Индиана значение числа пи на законодательном уровне приравнено к 4 — для удобства подсчётов. Мы проверили, правда ли это.
На постсоветском пространстве этот забавный факт известен ещё со времён СССР. Например, в 1991 году он попал в отечественное издание Книги рекордов Гиннесса со ссылкой на некий Билль 246, принятый Генеральной ассамблеей штата. И в наше время эта информация появляется в различных публикациях (часто — в сборниках нелепых американских законов). Например, в «Тверском лингвистическом меридиане», журнале «Новый крокодил» и таких авторитетных источниках, как журнал «Коммерсантъ Власть» и «Парламентская газета». А вот в книге «100 великих научных достижений России» приводится другое значение константы — там утверждается, что в штате Индиана число пи равно 3,2.
О том, что число пи (π) — соотношение длины окружности к её диаметру — иррационально, то есть не может быть представлено в виде обыкновенной дроби, люди знают со школьной скамьи. Обычно в бытовых расчётах используется округлённое значение — 3,14, хотя оно совсем не подходит для более точных и важных измерений.
Но давайте сначала обратимся не к проблемам числа пи, а к такой неразрешимой задаче древности, как квадратура круга — построении с помощью циркуля и линейки квадрата, равного по площади данному кругу. Математики бились над этой проблемой много веков, однако только в 1882 году Фердинанд фон Линдеман доказал тщетность всех потенциальных усилий в этом вопросе. И если учёные земного шара довольно быстро узнали о неутешительном, но в целом довольно ожидаемом выводе, то непрофессионалы не оставляли надежд.
В 1888 году врач и математик-любитель из Индианы Эдвард (Эдвин) Джонстон Гудвин решил, что совершил открытие, и потратил несколько лет на попытки сообщить о нём миру. В преддверии Всемирной выставки в Чикаго 1893 года ему удалось договориться с организаторами о выделении павильона для «чтения научных лекций». Однако вскоре руководство выставки, ознакомившись с выкладками Гудвина, известило его о своём отказе. Математик-любитель не унывал и в июле 1894 года опубликовал статью о своей научной победе не где-нибудь, а в «Американском математическом ежемесячнике», передовом издании в своей сфере. Правда, с пометкой «публикуется по запросу автора» и полным отказом об ответственности со стороны издания. Издатели не могли не видеть, что статья была полна ошибок. Во-первых, Гудвин не понимал, что задача заключается в построении равновеликого квадрата без измерительных приборов (линейка должна не иметь делений), а не в нахождении длины его стороны. Во-вторых, он утверждал, что площади круга и квадрата равны, если периметр последнего равен длине окружности, что, мягко говоря, неверно.
Так и не обнаружив в своих рассуждениях ошибок либо скрывая их, Эдвин Гудвин решил взять новую высоту. Он убедил Тейлора Рекорда, члена палаты представителей штата от своего родного округа Пози, выставить на рассмотрение Генеральной ассамблеи (аналог парламента) Индианы акт, который закреплял бы выводы Гудвина на законодательном уровне. Главный аргумент Гудвина заключался в том, что родная Индиана, благодаря его открытию, сможет сэкономить деньги. Ведь раз уж «правда» открылась, игнорировать её никто не сможет. А Гудвин собирался получать авторские отчисления за использование своего открытия (в первую очередь в учебных целях), но властям Индианы математический гений разрешил пользоваться его формулами бесплатно. Фермер и торговец лесом Тейлор Рекорд, проводивший свой первый и последний срок в качестве представителя, ничего не понял по математической части, но вскоре в палату представителей поступил Билль 246.
Этот билль выделялся множеством прекрасных деталей. Например, разделом 3, где говорилось, что гудвиновские решения проблем квадратуры круга, удвоения куба и трисекции угла (три неразрешимые классические задачи на построение) уже признаны вкладом в науку «Американским математическим ежемесячником». Как мы показали выше, это было неправдой.
Кроме того, нельзя пройти мимо фигуры, описанной в разделе 2:
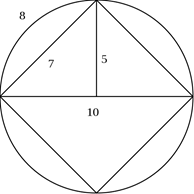
Это круг с длиной 32 и диаметром 10, в который вписан квадрат со стороной 7. Стороны изображённого квадрата, согласно теореме Пифагора, должны иметь длину:
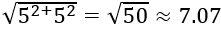
что не равно 7. Тем не менее Гудвин делает отсюда вывод, что длина окружности и диаметр соотносятся как 4 к 5/4, то есть, 3,2 к 1. И хотя число пи в законопроекте не фигурирует, из него следует, что эта константа равна 3,2. Не 4, а именно 3,2.
18 января 1897 года Билль 246 был рассмотрен палатой представителей штата Индиана. Тематика законопроекта и обилие незнакомых греческих слов вызвали некоторое замешательство среди народных избранников. Сначала было предложено отправить акт на одобрение в финансовый комитет. Затем — в комитет по болотам, где тот «найдёт заслуженную могилу». В конце концов бумага оказалась в ведении комитета по образованию, который, как ни странно, отозвался о проекте положительно, в результате чего 6 февраля 1897 года последний был принят палатой представителей (распределение голосов 67:0). Итак, половина дела была сделана, оставалось убедить Сенат.
Но на беду Эдвина Гудвина, днём ранее в Индианаполис прибыл профессор Кларенс Уолдо — заведующий отделением математики престижного университета Пердью, которому было поручено пролоббировать бюджет Академии наук штата. Меньше всего он ожидал попасть на обсуждение математического закона. Уолдо показали копию законопроекта и предложили познакомить с его автором. Профессор отказался, заявив, что его знакомили с достаточным количеством сумасшедших. Более того, он провёл серьёзный разговор с сенаторами, объяснив им реальное положение дел с квадратурой круга.
В итоге, когда законопроект дошёл до Сената, он был встречен там прохладно. Рассматривавший заявку комитет по трезвости дал своё одобрение, однако 12 февраля 1897 года Сенат отложил принятие билля на неопределённый срок. Решающим стал аргумент одного из сенаторов о том, что Генеральная ассамблея не обладает полномочиями определять математическую истину. Не последнюю роль сыграла и кампания по высмеиванию закона, развёрнутая в прессе:
Как писала Indianapolis News после решающего заседания, «сенаторы каламбурили по поводу закона и высмеивали его. Веселье длилось полчаса. Сенатор Хаббелл заявил, что Сенату, чьи заседания обходятся штату в $250 в день, не пристало терять время на такие фривольности. По его словам, изучение ведущих газет Чикаго и востока страны подвело его к выводу, что законодательные органы Индианы выставили себя на посмешище теми мерами, которые уже приняты в отношении билля». С тех пор к скандальному законопроекту больше не возвращались.
20 лет спустя профессор Уолдо предположил, что только вмешательство Академии наук предотвратило это чудовищное деяние. «Если это вывод верен, — добавил он, — то один только этот акт предотвращения стоил для Индианы, ревнивой к своей честной славе, больше, чем весь её прошлый и будущий вклад в публикацию протоколов заседаний Академии наук».
Врач и математик-любитель Эдвин Гудвин умер в 1902 году, всего лишь через пять лет после нашумевшего случая с законопроектом. Как было сказано в его некрологе, «он думал, что совершил великое открытие, и хотел принести этим пользу миру. <…> Шли годы, и, когда он увидел, что детище его гения по-прежнему не принимается научным миром, его постигло разочарование, хотя он никогда не терял надежды и верил, что до конца своих дней увидит, как мир осознал величие его плана, и насладится минутой славы. Его чаяниям не суждено было сбыться, и в мирных интерьерах деревенской жизни разыгралась трагедия бесплодных амбиций».
Как видим, несмотря на все драматические события, развернувшиеся вокруг проблемы квадратуры круга, законодательный орган штата Индиана так окончательно и не принял решения относительно числа пи и подобный закон никогда не действовал и не действует.
Большей частью ложь
Почитать по теме:
1. In Celebration of Pi Day: The History of the Indiana Pi Bill
2. House Bill No. 246, Indiana State Legislature
3. Hallenberg, Arthur E. House Bill No. 246 Revisited.
Интересное по теме: Без рубрики
Правда ли, что командующий войсками химзащиты РФ назвал мРНК-вакцины биологическим оружием?
В середине марта 2023 года в СМИ распространилась информация, что начальник войск радиационной, химической и биологической защиты РФ генерал-лейтенант Игорь Кириллов обвинил США в том, что разрабатываемые там мРНК-вакцины — это биологическое оружие. Мы решили проверить, правда ли военачальник заявлял подобное.
Правда ли, что если есть яблоки с косточками, то можно отравиться?
Считается, что косточки яблок настолько ядовиты, что, если съесть фрукт вместе с ними, можно получить тяжёлое отравление. Мы решили проверить, действительно ли косточки этих плодов такие опасные.
Правда ли, что многодетные матери живут дольше?
В начале марта 2023 года российские СМИ растиражировали слова эксперта Минздрава РФ, которая заявила, что продолжительность жизни женщины увеличивается, если она рожает много детей. Мы решили проверить, подтверждается ли такое высказывание научными данными.
